预计阅读本页时间:-
7.2.2 音频编码
音频(声音)波是一维的声(压)波。当声波进入人耳的时候,鼓膜将振动,导致内耳的小骨随之振动,将神经脉冲送入大脑,这些脉冲被收听者感知为声音。类似地,当声波冲击麦克风的时候,麦克风将产生电信号,将声音的振幅表示为时间的函数。
人耳可以听到的声音的频率范围从20 Hz到20 000Hz,而某些动物,特别是狗,能够听到更高频率的声音。耳朵是以对数规律听声音的,所以两个振幅为A和B的声音的比率习惯以dB(分贝)为单位来表示,公式为
dB=20 log10 (A/B)
广告:个人专属 VPN,独立 IP,无限流量,多机房切换,还可以屏蔽广告和恶意软件,每月最低仅 5 美元
如果我们定义1 kHz正弦波可听度的下限(压力大约为0.0003 dyne/cm2 )为0 dB,那么日常谈话大约为50 dB,而使人感到痛苦的阈值大约为120 dB,动态范围为一百万量级。为避免混淆,上面公式中的A和B是振幅。如果我们使用的是功率水平,则上面公式中对数前面的系数应该为10,而不是20,因为功率与振幅的平方成正比。
音频波可以通过模数转换器(Analog Digital Converter,ADC)转换成数字形式。ADC以电压作为输入,并且生成二进制数作为输出。图7-5a中为一个正弦波的例子。为了数字化地表示该信号,我们可以每隔∆T秒对其进行采样,如图7-5b中的条棒高度所示。如果一个声波不是纯粹的正弦波,而是正弦波的线性叠加,其中存在的最高频率成分为f,那么以2f的频率进行采样就足够了。1924年贝尔实验室的一位物理学家Harry Nyquist从数学上证明了这一结果,这就是著名的Nyquist抽样定理。更多地进行采样是没有价值的,因为如此采样可以检测到的更高的频率并不存在。
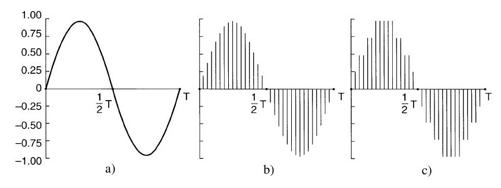
数字样本是不准确的。图7-5c中的样本只允许9个值,从-1.00到1.00,步长为0.25,因此,需要4个二进制位来表示它们。8位样本可以有256个不同的值,16位样本可以有65 536个不同的值。由于每一样本的位数有限而引入的误差称为量化噪声(quantization noise)。如果量化噪声太大,耳朵就会感觉到。
对声音进行采样的两个著名的例子是电话和音频CD。电话系统使用的是脉冲编码调制(pulse code modulation),脉冲编码调制每秒以7位(北美和日本)或8位(欧洲)对声音采样8000次,故这一系统的数据率为56 000 bps或64 000 bps。由于每秒只有8000个样本,所以4 kHz以上的频率就丢失了。
音频CD是以每秒44 100个样本的采样率进行数字化的,足以捕获最高达到22 050 Hz的频率,这对于人而言是很好的,但是对于狗而言却是很差的。每一样本在其振幅范围内以16位进行线性量化。注意,16位样本只有65 536个不同的值,而人耳以最小可听度为步长进行测量时的动态范围大约为一百万。所以每个样本只有16位引入了某些量化噪声(尽管没有覆盖全部动态范围,但是人们并不认为CD的质量受到损害)。以每秒44 100个样本、每个样本16位计算,音频CD需要的带宽单声道为705.6 Kbps,立体声为1.411 Mbps(参见图7-2)。音频压缩也许要以描述人类听觉如何工作的心理声学模型为基础。使用MPEG第3层(MP3)系统进行10倍的压缩是可能的。采用这一格式的便携式音乐播放器近年来已经十分普遍。
数字化的声音可以十分容易地在计算机上用软件进行处理。有许许多多的个人计算机程序可以让用户从多个信号源记录、显示、编辑、混合和存储声波。事实上,所有专业的声音记录与编辑系统如今都是数字化的。模拟方式基本上过时了。










