预计阅读本页时间:-
7.7.4 在单个磁盘上存放多个文件
到目前为止我们还只考虑了单部电影的存放。在视频服务器上,当然存在着许多电影。如果它们随机地散布在磁盘上,那么当多部电影被不同的客户同时观看时,时间将浪费在磁头在电影之间来回移动上。
通过观察到某些电影比其他电影更为流行并且在磁盘上存放电影时将流行性考虑进去,可以改进这一情况。尽管总的来说有关个别电影的流行性并没有多少可说的(除了有大腕明星似乎有所帮助以外),但是大体上关于电影的相对流行性总还是可以说出一些规律。
对于许多种类的流行性比赛,诸如出租的电影、从图书馆借出的图书、访问的Web网页,甚至一部小说中使用的英文单词或者特大城市居住的人口,相对流行性的一个合理的近似遵循着一种令人惊奇的可预测模式。这一模式是哈佛大学的一位语言学教授George Zipf(1902-1950)发现的,现在被称为Zipf定律。该定律说的是,如果电影、图书、Web网页或者单词按其流行性进行排名,那么下一个客户选择排行榜中排名为k的项的概率是C/k,其中C是一个归一化常数。
广告:个人专属 VPN,独立 IP,无限流量,多机房切换,还可以屏蔽广告和恶意软件,每月最低仅 5 美元
因而,前三部电影的命中率分别是C/1、C/2和C/3,其中C的计算要使全部项的和为1。换句话说,如果有N部电影,那么
C/1+C/2+C/3+C/4+…+C/N=1
从这一公式,C可以被计算出来。对于具有10个、100个、1000个和10 000个项的总体,C的值分别是0.341、0.193、0.134和0.102。例如,对于1000部电影,前5部电影的概率分别是0.134、0.067、0.045、0.034和0.027。
图7-22说明了Zipf定律。只是为了娱乐,该定律被应用于美国20座最大城市的人口。Zipf定律预测第二大城市应该具有最大城市一半的人口,第三大城市应该具有最大城市三分之一的人口,以此类推。虽然不尽完美,该定律令人惊奇地吻合。
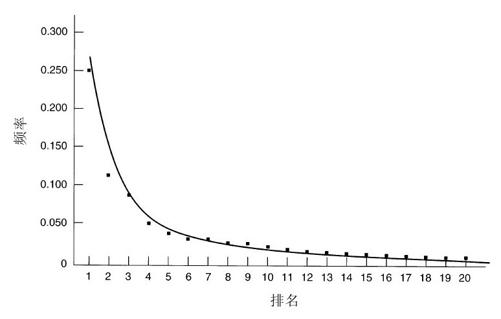
对于视频服务器上的电影而言,Zipf定律表明最流行的电影被选择的次数是第二流行的电影的两倍,是第三流行的电影的三倍,以此类推。尽管分布在开始时下降得相当快,但是它有着一个长长的尾部。例如,排名50的电影拥有C/50的流行性,排名51的电影拥有C/51的流行性,所以排名51的电影的流行性是排名50的电影的50/51,只有大约2%的差额。随着尾部进一步延伸,相邻电影间的百分比差额变得越来越小。一个结论就是,服务器需要大量的电影,因为对于前10名以外的电影存在着潜在的需求。
了解不同电影的相对流行性,使得对视频服务器的性能进行建模以及将该信息应用于存放文件成为可能。研究已经表明,最佳的策略令人惊奇地简单并且独立于分布。这一策略称为管风琴算法(organ-pipe algorithm)(Grossman和Silverman,1973;Wong,1983)。该算法将最流行的电影存放在磁盘的中央,第二和第三流行的电影存放在最流行的电影的两边,在这几部电影的外边是排名第四和第五的电影,以此类推,如图7-23所示。如果每一部电影是如图7-19所示类型的连续文件,这样的存放方式工作得最好;如果每一部电影被约束在一个狭窄的柱面范围之内,这样的存放方式也可以扩大其使用的范围。该算法的名字来自这样的事实——概率直方图看起来像是一个稍稍不对称的管风琴。
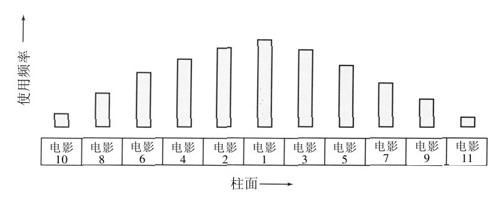
该算法所做的是试图将磁头保持在磁盘的中央。当服务器上的电影有1000部时,根据Zipf定律分布,排在前5名的电影代表了0.307的总概率,这意味着大约30%的时间磁头停留在为排在前5名的电影分配的柱面中,如果有1000部电影可用,这是一个惊人的数量。










