预计阅读本页时间:-
9.2.4 数字签名
经常性地使用数字签名是很有必要的。例如,假设银行客户通过发送电子邮件通知银行为其购买股票。一小时后,定单发出并成交,但随后股票大跌了。现在客户否认曾经发送过电子邮件。银行当然可以出示电子邮件作为证据,但是客户也可以声称是银行为了获得佣金而伪造了电子邮件。那么法官如何来找到真相呢?
通过对邮件或其他电子文档进行数字签名可以解决这类问题,并且保证了发送方日后不能抵赖。其中的一个通常使用的办法是首先对文档运行一种单向散列运算(hashing),这种运算几乎是不可逆的。散列函数通常独立于原始文档长度产生一个固定长度的结果值。最常用的散列函数有MD5(Message Digest 5),一种可以产生16个字节结果的算法(Rivest,1992)以及SHA-1(Secure Hash Algorithm),一种可以产生20个字节结果的算法(NIST,1995)。比SHA-1更新版本有SHA-256和SHA-512,它们分别产生32字节和64字节的散列结果,但是迄今为止,这两种加密算法依然没有得到广泛使用。
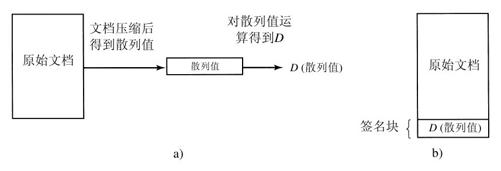
下一步假设我们使用上面讲过的公钥密码。文件所有者利用他的私钥对散列值进行运算得到D(散列值)。该值称为签名块(signature block),它被附加在文档之后传送给接收方,如图9-3所示。对散列值应用D有些像散列解密,但这并不是真正意义上的解密,因为散列值并没有被加密。这不过是对散列值进行的数学变换。
广告:个人专属 VPN,独立 IP,无限流量,多机房切换,还可以屏蔽广告和恶意软件,每月最低仅 5 美元
接收方收到文档和散列值后,首先使用事先取得一致的MD5或SHA算法计算文档的散列值,然后接收方使用发送方的公钥对签名块进行运算以得到E(D(hash))。这实际上是对解密后的散列进行“加密”,操作抵消,以恢复原有的散列。如果计算后的散列值与签名块中的散列值不一致,则表明:要么文档、要么签名块、要么两者共同被篡改过(或无意中被改动)。这种方法仅仅对一小部分数据(散列)运用了(慢速的)公钥密码体制。请注意这种方法仅仅对所有满足下面条件的x起作用:
E(D(x))=x
我们并不能保证所有的加密函数都拥有这种属性,因为我们原来所要求的就是:
D(E(x))=x
在这里,E是加密函数,D是解密函数。而为了满足签名的要求,函数运算的次序是不受影响的。也就是说,D和E一定是可交换的函数。而RSA算法就有这种属性。
要使用这种签名机制,接收方必须知道发送方的公钥。有些用户在其Web网页上公开他们的公钥,但是其他人并没有这么做,因为他们担心入侵者会闯入并悄悄地改动其公钥。对他们来说,需要其他方法来发布公钥。消息发送方的一种常用方法是在消息后附加数字证书,证书中包含了用户姓名、公钥和可信任的第三方数字签名。一旦用户获得了可信的第三方认证的公钥,那么对于所有使用这种可信第三方确认来生成自己证书的发送方,该用户都可以使用他们的证书。
认证机构(Certification Authority,CA)作为可信的第三方,提供签名证书。然而如果用户要验证有CA签名的证书,就必须得到CA的公钥,从哪里得到这个公钥?即使得到了用户又如何确定这的确是CA的公钥呢?为了解决上述两个问题,需要一套完整的机制来管理公钥,这套机制叫做PKI(Public Key Infrastructure,公钥基础设施)。网络浏览器已经通过一种特别的方式解决了这个问题:所有的浏览器都预加载了大约40个著名CA的公钥。
上面我们叙述了可用于数字证书的公钥密码体制。同时,我们也有必要指出不包含公钥体制的密码体系同样存在。










