预计阅读本页时间:-
本章我们将介绍一种新的编程范式:函数式编程(Functional Programming)。函数式编程历史悠久,但其使用一直限于学术圈。随着近年来并行运算的发展,人们发现古老的函数式编程天生地适用于并行运算。函数式编程变得越来越受欢迎。Python虽然不是纯粹的函数式编程,但包含了不少函数式编程的语法。了解函数式编程的概念,有助于写出更加优秀的代码。
7.1 又见函数
1.Python中的函数式
在前面,我们已经见到了面向过程和面向对象两种编程范式。面向过程编程利用选择和循环结构,以及函数、模块等,对指令进行封装。面向对象实现了另一种形式的封装。包含有数据的对象的一系列方法。这些方法能造成对象的状态改变。作为第三种编程范式,函数式编程的本质也在于封装。
正如其名字,函数式编程以函数为中心进行代码封装。在面向过程的编程中,我们已经见识过函数。它有参数和返回值,分别起到输入和输出数据的功能。更进一步,我们也已经知道Python中的函数实际上是一些特殊的对象。这一条已经符合了函数式编程的一个重要方面:函数是第一级对象,能像普通对象一样使用。我将在后面章节中探索它的重要意义。
广告:个人专属 VPN,独立 IP,无限流量,多机房切换,还可以屏蔽广告和恶意软件,每月最低仅 5 美元
函数式编程强调了函数的纯粹性(purity)。一个纯函数是没有副作用的(Side Effect),即这个函数的运行不会影响其他函数。纯函数像一个沙盒,把函数带来的效果控制在内部,从而不影响程序的其他部分。我们曾在函数内部改变外部列表的元素,其他调用该列表的函数也会看到该函数的作用效果。这样就造成了副作用。我们知道,造成这样效果的原因是我们使用了可变更的对象,如列表和词典。因此,为了达到纯函数的标准,函数式编程要求其变量都是不可变更的。
Python并非完全的函数式编程语言。在Python中,存在着可变更的对象,也能写出非纯函数。但如果我们借鉴函数式编程,尽量在编程中避免副作用,就会有许多好处。由于纯函数相互独立,我们不用担心函数调用对其他函数的影响,所以使用起来更加简单。另外一点,纯函数也方便进行并行化运算。在并行化编程时,我们经常要担心不同进程之间相互干扰的问题。当多个进程同时修改一个变量时,进程的先后顺序会影响最终结果。比如下面两个函数:
from threading import Thread
x = 5
def double():
global x
x = x * 2
def plus_ten():
global x
x = x + 10
thread1 = Thread(target=double)
thread2 = Thread(target=plus_ten)
thread1.start()
thread2.start()
thread1.join()
thread2.join()
print(x)
上面的两个函数中使用了关键字global。global说明了x是一个全局变量。函数对全局变量的修改能被其他函数看到,因此有副作用。如果两个进程并行地执行两个函数,函数的执行顺序不确定,则结果可能是double()中的x = x*2先执行,最终结果为20;也有可能是plus_ten()中的x = x + 10先执行,最终结果为30。这被称为竞跑条件(Race Condition),是并行编程中需要极力避免的。
函数式编程消灭了副作用,即无形中消除了竞跑条件的可能。因此,函数式编程天生地适用于并行化运算。其实函数式编程诞生得很早,早在20世纪50年代,Lisp语言就已经诞生。但函数式编程的使用范围局限于学术领域。近年来,电子元件的尺寸已经趋于物理极限。CPU频率的增长逐渐放缓。为了满足运算的需要,人们想到了把多个电脑连接起来,用并行化的方式来提高运算能力。但并行程序与之前的单线程程序有很大区别,程序员要处理竞跑条件等复杂问题。饱受折磨的程序员想起了古董级的函数式编程语言,意外地发现它十分适合于编写并行程序。于是,函数式编程重拾热度,渐渐成为程序员的必修内容。
Python并非一门函数式编程语言。在早期的Python版本中,并没有函数式编程的相关语法。后来Python中加入了lambda函数,以及map、filter、reduce等高阶函数,从而加入了函数式编程的特征。但Python并没有严格地执行语法规范,并且缺乏相关的优化,因此离完整的函数式编程尚有一段距离。Python的作者罗苏姆本人也从不认为Python是一门函数式语言。作为一名渐进式的开发者,罗苏姆非常看重程序的可读性。因此,他只保留了函数式编程中那些让Python更加简洁的语法糖。所以,Python中函数式语法特征可以作为体验的起点。但这还远远不够,你至少应该去深入了解函数式编程的思想。更好的情况是,你能学习一门更加纯粹的函数式语言,与Python中的所学互为对照。
在我的体会中,学习函数式编程能深刻地影响编程的思维方式。程序员编程时,很多时候是自下而上的:创建一个变量,给变量赋值,进行运算,得到结果……这是一种很自然的想法。程序员毕竟是在摆弄机器,因此第一步总会像第一次玩收音机一样,转转按钮、动动天线,看一下机器是什么反应。与之相对,函数式编程的思路是自上而下的。它先提出一个大问题,在最高层用一个函数来解决这个大问题。在这个函数内部,再用其他函数来解决小问题。在这样递归式的分解下,直到问题得到解决。这就好像“把大象放入冰箱”这个函数,在内部调用“打开门”、“把大象放进去”、“关上门”这三个函数。在这三个内部函数中,可以继续通过函数调用,向细节深入。这两种思维方式各有利弊,但让它们相互对比、相互碰撞,是学习编程的一大乐趣。
2.并行运算
在上一节中,我们已经涉及到并行运算。所谓的并行运算,是指多条指令同时执行。一般来说,一台单处理器的计算机同一时间内只能执行一条指令。这种每次执行一条指令的工作方式称为串行运算。

图7-1 串行运算:必须一个一个来
大规模并行运算通常是在有多个主机组成的集群(Cluster)上进行的。主机之间可以借助高速的网络设备通信。一个集群的造价不菲。然而,我们可以在单机上通过多进程或多线程的方式,模拟多主机的并行处理。即使一台单机中,也往往存在着多个运行着的程序,即所谓的进程。例如,我们在打开浏览器上网的同时,还可以流畅的听音乐。这给我们一个感觉,计算机在并行的进行上网和放音乐两个任务。事实上,单机的处理器按照“分时复用”的方式,把运算能力分配给多个进程。处理器在进程间频繁切换。因此,即使处理器同一时间只能处理一个指令,但通过在进程间的切换,也能造成多个进程齐头并进的效果。
图7-2 并行运算:可以齐头并进
从这个角度来说,集群和单机都实现了多个进程的并行运算。只不过,集群上的多进程分布在不同的主机,而单机的多进程存在于同一主机,并借着“分时复用”来实现并行。
下面是多进程编程的一个例子:
import multiprocessing
def proc1():
return 999999**9999
def proc2():
return 888888**8888
p1 = multiprocessing.Process(target=proc1)
p2 = multiprocessing.Process(target=proc2)
p1.start()
p2.start()
p1.join()
p2.join()
上面程序用了两个进程。进程的工作包含在函数中,分别是函数proc1()和函数proc2()。方法start()用于启动进程,而join()方法用于在主程序中等待相应进程完成。
最后,我们要区分一下多进程和多线程。一个程序运行后,就成为一个进程。进程有自己的内存空间,用来存储自身的运行状态、数据和相关代码。一个进程一般不会直接读取其他进程的内存空间。进程运行过程中,可以完成程序描述的工作。但在一个进程内部,又可以有多个称为“线程”的任务,处理器可以在多个线程之间切换,从而形成并行的多线程处理。线程看起来和进程类似,但线程之间可以共享同一个进程的内存空间。
7.2 被解放的函数
1.函数作为参数和返回值
在函数式编程中,函数是第一级对象。所谓“第一级对象”,即函数能像普通对象一样使用。因此,函数的使用变得更加自由。对于“一切皆对象”的Python来说,这是自然而然的结果。既然如此,那么函数可以像一个普通对象一样,成为其他函数的参数。比如下面的程序,函数就充当了参数:
def square_sum(a, b):
return a**2 + b**2
def cubic_sum(a, b):
return a**3 + b**3
def argument_demo(f, a, b):
return f(a, b)
print(argument_demo(square_sum, 3, 5)) # 打印34
print(argument_demo(cubic_sum, 3, 5)) # 打印152
函数argument_demo()的第一个参数f就是一个函数对象。按照位置传参,square_sum()传递给函数argument_demo(),对应参数列表中的f。f会在argument_demo()中被调用。我们可以把其他函数,如cubic_sum()作为参数传递给argument_demo()。
很多语言都能把函数作为参数使用,例如C语言。在图形化界面编程时,这样一个作为参数的函数经常起到回调(Callback)的作用。当某个事件发生时,比如界面上的一个按钮被按下,回调函数就会被调用。下面是一个GUI回调的例子:
import tkinter as tk
def callback():
"""
callback function for button click
"""
listbox.insert(tk.END, "Hello World!")
if __name__ == "__main__":
master = tk.Tk()
button = tk.Button(master, text="OK", command=callback)
button.pack()
listbox = tk.Listbox(master)
listbox.pack()
tk.mainloop()
Python中内置了tkinter的图形化功能。在上面的程序中,回调函数将在列表栏中插入"Hello World!"。回调函数作为参数传给按钮的构造器。每当按钮被点击时,回调函数就会被调用,如图7-3所示。
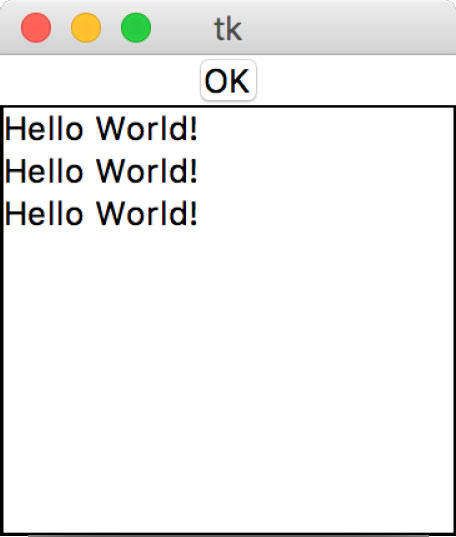
图7-3 回调函数运行结果
2.函数作为返回值
既然函数是一个对象,那么它就可以成为另一个函数的返回结果。
def line_conf():
def line(x):
return 2*x+1
return line # return a function object
my_line = line_conf()
print(my_line(5)) # 打印11
上面的代码可以成功运行。line_conf()的返回结果被赋给line对象。上面的代码将打印11。
在上面的例子中,我们看到了在一个函数内部定义的函数。和函数内部的对象一样,函数对象也有存活范围,也就是函数对象的作用域。Python的缩进形式很容易让我们看到函数对象的作用域。函数对象的作用域与它的def的缩进层级相同。比如下面的代码,我们在line_conf()函数的隶属范围内定义的函数line(),就只能在line_conf()的隶属范围内调用。
def line_conf():
def line(x):
return 2*x+1
print(line(5)) #作用域内
if __name__=="__main__":
line_conf()
print(line(5)) #作用域外,报错
函数line()定义了一条直线(y = 2x + 1)。可以看到,在line_conf()中可以调用line()函数,而在作用域之外调用line()函数将会有下面的错误:
NameError: name 'line' is not defined
说明这已经超出了函数line()的作用域。Python对该函数的调用失败。
3.闭包
上面函数中,line()定义嵌套在另一个函数内部。如果函数的定义中引用了外部变量,会发生什么呢?
def line_conf():
b = 15
def line(x):
return 2*x+b
b = 5
return line #返回函数对象
if __name__ == "__main__":
my_line = line_conf()
print(my_line(5)) # 打印15
可以看到,line()定义的隶属程序块中引用了高层级的变量b。b的定义并不在line()的内部,而是一个外部对象。我们称b为line()的环境变量。尽管b位于line()定义的外部,但当line被函数line_conf()返回时,还是会带有 b的信息。
一个函数和它的环境变量合在一起,就构成了一个闭包(Closure)。上面程序中,b分别在line()定义的前后有两次不同的赋值。上面的代码将打印15,也就是说,line()参照的是值为5的b值。因此,闭包中包含的是内部函数返回时的外部对象的值。
在Python中,所谓的闭包是一个包含有环境变量取值的函数对象。环境变量取值被复制到函数对象的__closure__属性中。比如下面的代码:
def line_conf():
b = 15
def line(x):
return 2*x+b
b = 5
return line # 返回函数对象
if __name__ == "__main__":
my_line = line_conf()
print(my_line.__closure__)
print(my_line.__closure__[0].cell_contents)
可以看到,my_line()的__closure__属性中包含了一个元组。这个元组中的每个元素都是cell类型的对象。第一个cell包含的就是整数5,也就是我们返回闭包时的环境变量b的取值。
闭包可以提高代码的可复用性。我们看下面三个函数:
def line1(x):
return x + 1
def line2(x):
return 4*x + 1
def line3(x):
return 5*x + 10
def line4(x):
return -2*x – 6
如果把上面的程序改为闭包,那么代码就会简单很多:
def line_conf(a, b):
def line(x):
return a*x + b
return line
line1 = line_conf(1, 1)
line2 = line_conf(4, 5)
line3 = line_conf(5, 10)
line4 = line_conf(-2, -6)
这个例子中,函数line()与环境变量a、b构成闭包。在创建闭包的时候,我们通过line_conf()的参数a、b说明直线的参量。这样,我们就能复用同一个闭包,通过代入不同的数据来获得不同的直线函数,如y = x + 1和y = 4x + 5。闭包实际上创建了一群形式相似的函数。
除了复用代码,闭包还能起到减少函数参数的作用:
def curve_closure(a, b, c):
def curve(x):
return a*x**2 + b*x + c
return curve
curve1 = curve_closure(1, 2, 1)
函数curve()是一个二次函数。它除了自变量x外,还有a、b、c三个参数。通过curve_closure()这个闭包,我们可以预设a、b、c三个参数的值。从而起到减参的效果。
闭包的减参作用对于并行运算来说很有意义。在并行运算的环境下,我们可以让每台电脑负责一个函数,把上一台电脑的输出和下一台电脑的输入串联起来。最终,我们像流水线一样工作,从串联的电脑集群一端输入数据,从另一端输出数据。由于每台电脑只能接收一个输入,所以在串联之前,必须用闭包之类的办法把参数的个数降为1。
7.3 小女子的梳妆匣
1.装饰器
装饰器(decorator)是一种高级Python语法。装饰器可以对一个函数、方法或者类进行加工。在Python中,我们有多种方法对函数和类进行加工。装饰器从操作上入手,为函数增加额外的指令。因此,装饰器看起来就像是女孩子的梳妆匣,一番打扮之后让函数大变样。Python最初没有装饰器这一语法。装饰器在Python 2.5中才出现,最初只用于函数。在Python 2.6以及之后的Python版本中,装饰器被进一步用于类。
我们先定义两个简单的数学函数,一个用来计算平方和,一个用来计算平方差:
# 获得平方和
def square_sum(a, b):
return a**2 + b**2 # get square diff
# 获得平方差
def square_diff(a, b):
return a**2 - b**2
if __name__ == "__main__":
print(square_sum(3, 4)) # 打印25
print(square_diff(3, 4) # 打印-7
在拥有了基本的数学功能之后,我们可能想为函数增加其他的功能,比如打印输入。我们可以改写函数来实现这一点:
# 装饰:打印输入
def square_sum(a, b):
print("intput:", a, b)
return a**2 + b**2
def square_diff(a, b):
print("input", a, b)
return a**2 - b**2
if __name__ == "__main__":
print(square_sum(3, 4))
print(square_diff(3, 4))
我们修改了函数的定义,为函数增加了功能。从代码中可以看到,这两个函数在功能上的拓展有很高的相似性,都是增加了print("input", a, b)这一打印功能。我们可以改用装饰器,定义功能拓展本身,再把装饰器用于两个函数:
def decorator_demo(old_function):
def new_function(a, b):
print("input", a, b) # 额外的打印操作
return old_function(a, b)
return new_function
@decorator_demo
def square_sum(a, b):
return a**2 + b**2
@decorator_demo
def square_diff(a, b):
return a**2 - b**2
if __name__ == "__main__":
print(square_sum(3, 4))
print(square_diff(3, 4))
装饰器可以用def的形式定义,如上面代码中的decorator_demo()。装饰器接收一个可调用对象作为输入参数,并返回一个新的可调用对象。装饰器新建了一个函数对象,也就是上面的new_function()。在new_function()中,我们增加了打印的功能,并通过调用old_function(a, b)来保留原有函数的功能。
定义好装饰器后,我们就可以通过@语法使用了。在函数square_sum()和square_diff()定义之前调用@decorator_demo,实际上是将square_sum()或square_diff()传递给了decorator_demo(),并将decorator_demo()返回的新的函数对象赋给原来的函数名square_sum()和square_diff()。所以,当我们调用square_sum(3, 4)的时候,实际上发生的是:
square_sum = decorator_demo(square_sum) square_sum(3, 4)
我们知道,Python中的变量名和对象是分离的。变量名其实是指向一个对象的引用。从本质上,装饰器起到的作用就是名称绑定(name binding),让同一个变量名指向一个新返回的函数对象,从而达到修改函数对象的目的。只不过,我们很少彻底地更改函数对象。在使用装饰器时,我们往往会在新函数内部调用旧的函数,以便保留旧函数的功能。这也是“装饰”名称的由来。
下面看一个更有实用功能的装饰器。我们可以利用time包来测量程序运行的时间。把测量程序运行时间的功能做成一个装饰器,将这个装饰器运用于其他函数,将显示函数的实际运行时间:
import time
def decorator_timer(old_function):
def new_function(*arg, **dict_arg):
t1 = time.time()
result = old_function(*arg, **dict_arg)
t2 = time.time()
print("time: ", t2 - t1)
return result
return new_function
在new_function()中,除调用旧函数外,还前后额外调用了一次time.time()。由于time.time()返回挂钟时间,它们的差值反映了旧函数的运行时间。此外,我们通过打包参数的办法,可以在新函数和旧函数之间传递所有的参数。
装饰器可以实现代码的可复用性。我们可以用同一个装饰器修饰多个函数,以便实现相同的附加功能。比如说,在建设网站服务器时,我们能用不同函数表示对不同HTTP请求的处理。当我们在每次处理HTTP请求前,都想附加一个客户验证功能时,那么就可以定义一个统一的装饰器,作用于每一个处理函数。这样,程序能重复利用,可读性也大为提高。
2.带参装饰器
在上面的装饰器调用中,比如@decorator_demo,该装饰器默认它后面的函数是唯一的参数。装饰器的语法允许我们调用decorator时,提供其他参数,比如@decorator(a)。这样,就为装饰器的编写和使用提供了更大的灵活性。
# 带参装饰器
def pre_str(pre=""):
def decorator(old_function):
def new_function(a, b):
print(pre + "input", a, b)
return old_function(a, b)
return new_function
return decorator
# 装饰square_sum()
@pre_str("^_^")
def square_sum(a, b):
return a**2 + b**2 # get square diff
# 装饰square_diff()
@pre_str("T_T")
def square_diff(a, b):
return a**2 - b**2
if __name__ == "__main__":
print(square_sum(3, 4))
print(square_diff(3, 4))
上面的pre_str是一个带参装饰器。它实际上是对原有装饰器的一个函数封装,并返回一个装饰器。我们可以将它理解为一个含有环境参量的闭包。当我们使用@pre_str("^_^")调用的时候,Python能够发现这一层的封装,并把参数传递到装饰器的环境中。该调用相当于:
square_sum = pre_str("^_^") (square_sum)
根据参数不同,带参装饰器会对函数进行不同的加工,进一步提高了装饰器的适用范围。还是以网站的用户验证为例子。装饰器负责验证的功能,装饰了处理HTTP请求的函数。可能有的关键HTTP请求需要管理员权限,有的只需要普通用户权限。因此,我们可以把“管理员”和“用户”作为参数,传递给验证装饰器。对于那些负责关键HTTP请求的函数,我们可以把“管理员”参数传给装饰器。对于负责普通HTTP请求的函数,我们可以把“用户”参数传给它们的装饰器。这样,同一个装饰器就可以满足不同的需求了。
3.装饰类
在上面的例子中,装饰器接收一个函数,并返回一个函数,从而起到加工函数的效果。装饰器还拓展到了类。一个装饰器可以接收一个类,并返回一个类,从而起到加工类的效果。
def decorator_class(SomeClass):
class NewClass(object):
def __init__(self, age):
self.total_display = 0
self.wrapped = SomeClass(age)
def display(self):
self.total_display += 1
print("total display", self.total_display)
self.wrapped.display()
return NewClass
@decorator_class
class Bird:
def __init__(self, age):
self.age = age
def display(self):
print("My age is",self.age)
if __name__ == "__main__":
eagle_lord = Bird(5)
for i in range(3):
eagle_lord.display()
在装饰器decorator_class中,我们返回了一个新类NewClass。在新类的构造器中,我们用一个属性self.wrapped记录了原来类生成的对象,并附加了新的属性total_display,用于记录调用display()的次数。我们也同时更改了display方法。通过装饰,我们的Bird类可以显示调用display()的次数。
无论是装饰函数,还是装饰类,装饰器的核心作用都是名称绑定。虽然装饰器端出现较晚,但在各个Python项目中的使用却很广泛。即便不需要自定义装饰器,你也很有可能会在自己的项目中调用其他库中的装饰器。因此,Python程序员需要掌握这一语法。
7.4 高阶函数
1.lambda与map
上面的讲解都围绕着一个中心,函数能像一个普通对象一样应用,从而成为其他函数的参数和返回值。能接收其他函数作为参数的函数,被称为高阶函数(high-order function)。7.3节中介绍的装饰器,本质上就是高阶函数。高阶函数是函数式编程的一个重要组成部分。本节我们讲介绍最具有代表性的高阶函数:map()、filter()和reduce()。
在开始之前,首先引入一种新的定义函数的方式。我们已经见过很多用def来定义函数的例子。除了def,还可以用lambda语法来定义匿名函数,例如:
lambda_sum = lambda x,y: x + y print(lambda_sum(3,4))
通过lambda,我们创建了一个匿名的函数对象。借着赋值语句,这个匿名函数赋予给函数名lambda_sum。函数的参数为x、y,返回值为x与y的和。函数lambda_sum()的调用与正常函数一样。这种用lambda来产生匿名函数的方式适用于简短函数的定义。
现在我们来看高阶函数。所谓高阶函数,就是能处理函数的函数。在第1章中,我们就已经见过了函数对象参数。那个接收函数对象为参数的函数,就是高阶函数。Python中提供了很多有用的高阶函数。我们从map()开始介绍。函数map()是Python的内置函数。它的第一个参数就是一个函数对象。函数map()把这一个函数对象作用于多个元素:
data_list = [1,3,5,6] result= map(lambda x: x+3,data_list)
函数map()的第二个参数是一个可循环对象。对于data_list的每个元素, lambda函数都会调用一次。那个元素会成为lambda函数的参数。换个角度说,map()把接收到的函数对象依次作用于每一个元素。最终,map()会返回一个迭代器(1)。迭代器中的元素,就是多次调用lambda函数的结果。因此,上面的代码相当于:
def equivalent_generator(func, iter):
for item in iter:
yield func(item)
data_list = [1,3,5,6]
result = map(lambda x: x+3, data_list)
上面的lambda函数只有一个参数。这个函数也可以是一个多参数的函数。这个时候,map()的参数列表中就需要提供相应数目的可循环对象。
def square_sum(x, y):
return x**2 + y**2
data_list1 = [1,3,5,7]
data_list2 = [2,4,6,8]
result= map(square_sum,data_list1, data_list2)
这里,map()接收了square_sum()作为第一个参数。数square_sum()要求有两个参数。因此,map()调用时需要两个可循环对象。第一个循环对象提供了square_sum()中对应于x的参数,第二个循环对象提供了对应于y的参数。它们的关系如图7-3所示。
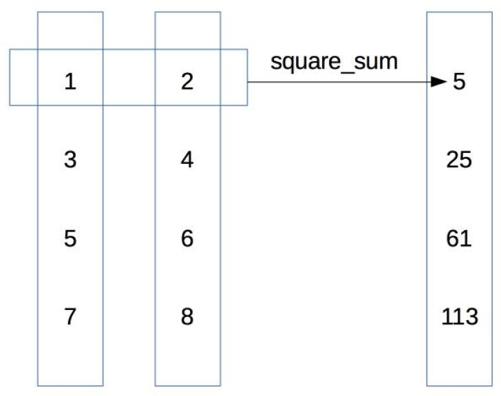
图7-3 两个循环对象之间的关系
一定程度上,map()函数能替代循环的功能。用map()函数写出的程序,看起来也相当简洁。从另一个角度来说,map()看起来像是对多个目标“各个击破”。在并行运算中,Map是一个很重要的过程。通过Map这一步,一个大问题可以分拆成很多小问题,从而能交给不同的主机处理。例如在图像处理中,就可以把一张大图分拆成许多张小图。每张小图分配给一台主机处理。
2.filter函数
和map()函数一样,内置函数filter()的第一个参数也是一个函数对象。它也将这个函数对象作用于可循环对象的多个元素。如果函数对象返回的是True,则该次的元素被放到返回的迭代器中。也就是说,filter()通过调用函数来筛选数据。
下面是使用filter()函数的一个例子。作为参数的larger100()函数用于判断元素是否比100大:
def larger100(a):
if a > 100:
return True
else:
return False
for item in filter(larger100,[10,56,101,500]):
print(item)
类似的,filter()用于多参数的函数时,也可以在参数中增加更多的可循环对象。总的来说,map()函数和filter()函数的功能有相似的地方,都是把同一个函数应用于多个数据。
3.reduce函数
函数reduce()也是一个常见的高阶函数。函数reduce()在标准库的functools包中(2),使用之前需要引入。和map()、reduce()一样,reduce()函数的第一个参数是函数,但reduce()对作为参数的函数对象有一个特殊要求,就是这个作为参数的函数必须能接收两个参数。Reduce()可以把函数对象累进的作用于各个参数。这个功能可以用一个简单的例子来说明:
from functools import reduce
data_list = [1,2,5,7,9]
result = reduce(lambda x, y: x + y, data_list)
print(result) # 打印24
函数reduce()的第一个参数是求和的sum()函数,它接收两个参数x和y。在功能上,reduce()累进的运用传给它的二参函数。上一次运算的结果将作为下一次调用的第一个参数。首先,reduce()将用表中的前两个元素1和2做sum()函数的参数,得到3。该返回值3将作为sum()函数的第一个参数,而将表中的下一个元素5作为sum()函数的第二个参数,进行下一次求和得到8。8会成为新的参数,与下一个元素7求和。上面过程不断重复,直到列表中元素耗尽。函数reduce()将返回累进的运算结果,这里是一个单一的整数。上面的例子相当于(((1+2)+5)+7)+9,结果为24。也就是如图7-4所示过程。
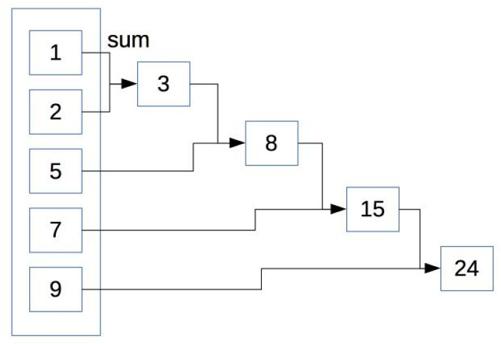
图7-4 累进运算过程
函数reduce()通过某种形式的二元运算,把多个元素收集起来,形成一个单一的结果。上面的map()、reduce()函数都是单线程的,所以运行效果和循环差不多。但map()、reduce()可以方便地移植到并行化的运行环境下。在并行运算中,Reduce运算紧接着Map运算。Map运算的结果分布在多个主机上,Reduce运算把结果收集起来。因此,谷歌用于并行运算的软件架构,就称为MapReduce(3)。
4.并行处理
下面的程序就是在多进程条件下使用了多线程的map()方法。这段程序多线程地下载同一个URL下的资源。程序用了第三方包requests来进行HTTP下载:
import time
from multiprocessing import Pool
import requests
def decorator_timer(old_function):
def new_function(*arg, **dict_arg):
t1 = time.time()
result = old_function(*arg, **dict_arg)
t2 = time.time()
print("time: ", t2 - t1)
return result
return new_function
def visit_once(i, address="http://www.cnblogs.com"):
r = requests.get(address)
return r.status_code
@decorator_timer
def single_thread(f, counts):
result = map(f, range(counts))
return list(result)
@decorator_timer
def multiple_thread(f, counts, process_number=10):
p = Pool(process_number)
return p.map(f, range(counts))
if __name__ == "__main__":
TOTAL = 100
print(single_thread(visit_once, TOTAL))
print(multiple_thread(visit_once, TOTAL))
在上面的程序中,我们启动了10个进程,并行地处理100个下载需求。这里把单个下载过程描述为一个函数,即visit_once(),然后用多线程的map()方法,把任务分配给雇佣来的10个工人,也就是10个进程。从结果可以看到,运行时间能大为缩短。
7.5 自上而下
1.便捷表达式
在本章的一开始,我们就提到函数式编程的思维是自上而下式的。Python中也有不少体现这一思维的语法,如生成器表达式、列表解析和词典解析。生成器表达式是构建生成器的便捷方法。考虑下面一个生成器:
def gen():
for i in range(4):
yield i
等价的,上面程序可以写成生成器表达式(Generator Expression):
gen = (x for x in range(4))
这一语法很直观,写出来的代码也很简洁。
我们再来看看生成一个列表的方法:
l = []
for x in range(10):
l.append(x**2)
上述代码生成了表l,但有更快的方式。列表解析(List Comprehension)是快速生成列表的方法。它的语法简单,很有实用价值。列表解析的语法和生成器表达式很像,只不过把小括号换成了中括号:
l = [x**2 for x in range(10)]
列表解析的语法很直观。我们直截了当地说明了想要的是元素的平方,然后再通过for来增加限定条件,即哪些元素的平方。除了for,列表解析中还可以使用if。比如下面一个更复杂的例子:
xl = [1,3,5]
yl = [9,12,13]
l = [ x**2 for (x,y) in zip(xl,yl) if y > 10]
词典解析可用于快捷的生成词典。它的语法也与之前的类似:
d = {k: v for k,v in enumerate("Vamei") if val not in "Vi"}
你大概猜出它的结果了,可以在Python上验证一下。
2.懒惰求值
Python中的迭代器也很有函数式编程的意味。从功能上说,迭代器很多时候看起来就像一个列表。比如下面的迭代器和列表,效果上都一样:
for i in (x**2 for x in range(10)): print(i) for i in [x**2 for x in range(10)]: print(i)
但我们在介绍迭代器时曾提到过,迭代器的元素是实时计算出来的。在使用该元素之前,元素并不会占据内存空间。与之相对应,列表在建立时,就已经产生了各个元素的值,并保存在内存中。迭代器的工作方式正是函数式编程中的懒惰求值(Lazy Evaluation)。我们可以对迭代器进行各种各样的操作。但只有在需要时,迭代器才会计算出具体的值。
懒惰求值可以最小化计算机要做的工作。比如下面的程序可以在Python 3中飞速运行完成:
a = range(100000000)
result = map(lambda x: x**2, a)
在Python 3中,上面程序可以迅速执行。因为map返回的是迭代器,所以会懒惰求值(4)。更早之前的range调用返回的同样是迭代器,也是懒惰求值。除非通过某种方式调用迭代器中的元素,或者把迭代器转化成列表,运算过程才会开始。因此,在下面的程序中,如果把结果转化成列表,那么运算时间将大为增加。
a = range(100000000)
result = map(lambda x: x**2, a)
result = list(result)
如果说计算最终都不可避免,那么懒惰求值和即时求值的运算量并没有什么差别。但如果不需要穷尽所有的数据元素,那么懒惰求值将节省不少时间。比如下面的情况中,列表提前准备数据的方式,就浪费了很多运算资源:
for i in (x**2 for x in range(100000000)): if i>1000: break; for i in [x**2 for x in range(100000000)]: if i>1000: break;
除了运算资源,懒惰求职还能节约内存空间。对于即时求职来说,其运算过程的中间结果都需要占用不少的内存空间。而懒惰求值可以先在迭代器层面上进行操作,在获得最终迭代器以后一次性完成计算。除了用map()、filter()等函数外,Python中的itertools包还提供了丰富的操作迭代器的工具。
3.itertools包
标准库中的itertools包提供了更加灵活的生成迭代器的工具,这些工具的输入大都是已有的迭代器。另一方面,这些工具完全可以自行使用Python实现,该包只是提供了一种比较标准、高效的实现方式。这也符合Python“只有且最好只有一个解决方案”的理念。
#引入itertools
from itertools import *
这个包中提供了很多有用的生成器。下面两个生成器能返回无限循环的迭代器:
count(5, 2) #从5开始的整数迭代器,每次增加2,即5, 7, 9, 11, 13 ...
cycle("abc") #重复序列的元素,既a, b, c, a, b, c ...
repeat()既可以返回一个不断重复的迭代器,也可以是有次数限制的重复:
repeat(1.2) #重复1.2,构成无穷迭代器,即1.2, 1.2, 1.2, ... repeat(10, 5) #重复10,共重复5次
我们还能组合旧的迭代器,来生成新的迭代器:
chain([1, 2, 3], [4, 5, 7]) # 连接两个迭代器成为一个。1, 2, 3, 4, 5, 7
product("abc", [1, 2]) # 多个迭代器集合的笛卡儿积。相当于嵌套循环
所谓的笛卡儿积可以得出集合元素所有可能的组合方式:
for m, n in product("abc", [1, 2]):
print(m, n)
如下所示:
permutations("abc", 2) # 从"abcd"中挑选两个元素,比如ab, bc, ……
# 将所有结果排序,返回为新的迭代器。
#上面的组合区分顺序,即ab, ba都返回。
combinations("abc", 2) # 从"abcd"中挑选两个元素,比如ab, bc, ……
# 将所有结果排序,返回为新的迭代器。
# 上面的组合不区分顺序,
# 即ab, ba,只返回一个ab。
combinations_with_replacement("abc", 2) # 与上面类似,
# 但允许两次选出的元素重复。即多了aa, bb, cc
itertools包中还提供了许多有用的高阶函数:
starmap(pow, [(1, 1), (2, 2), (3, 3)]) # pow将依次作用于表的每个tuple。
takewhile(lambda x: x < 5, [1, 3, 6, 7, 1]) # 当函数返回True时,
#收集元素到迭代器。一旦函数返回False,则停止。1, 3
dropwhile(lambda x: x < 5, [1, 3, 6, 7, 1]) # 当函数返回False时,
#跳过元素。一旦函数返回True,则开始收集剩下的所有元素到迭代器。6, 7, 1
包中提供了groupby()函数,能将一个key()函数作用于原迭代器的各个元素,从而获得各个函数的键值。根据key()函数结果,将拥有元素分组。每个分组中的元素都保罗了键值形同的返回结果。函数groupby()分出的组放在一个迭代器中返回。
如果有一个迭代器,包含一群人的身高。我们可以使用这样一个key()函数: 如果身高大于180,返回"tall";如果身高低于160,返回"short";中间的返回"middle"。最终,所有身高将分为三个迭代器,即"tall"、"short"、"middle"。
from itertools import groupby
def height_class(h):
if h > 180:
return "tall"
elif h < 160:
return "short"
else:
return "middle"
friends = [191, 158, 159, 165, 170, 177, 181, 182, 190]
friends = sorted(friends, key = height_class)
for m, n in groupby(friends, key = height_class):
print(m)
print(list(n))
注意,groupby()的功能类似于UNIX中的uniq命令。分组之前需要使用sorted()对原迭代器的元素,根据key()函数进行排序,让同组元素先在位置上靠拢。
这个包中还有其他一些工具,方便迭代器的构建:
compress("ABCD", [1, 1, 1, 0]) #根据[1, 1, 1, 0]的真假值情况,选择
#保留第一个参数中的元素。A, B, C
islice() # 类似于slice()函数,只是返回的是一个迭代器
izip() # 类似于zip()函数,只是返回的是一个迭代器。
至此,本书介绍了Python中包含的函数式编程特征:作为第一级对象的函数、闭包、高阶函数、懒惰求值……这些源于函数式编程的语法,以函数核心提供了一套新的封装方式。当我们编程时,可以在面向过程和面向对象之外,提供一个新的选择,从而给程序更大的创造空间。函数式编程自上而下的思维,也给我们的编程带来更多启发。在并行运算的发展趋势下,函数式编程正走向繁荣。希望本章的内容能对你的函数式编程学习有所助益。
————————————————————
(1) 在Python 2.7中,map()返回的是一个列表
(2) Python 2.7中,reduce()是内置函数,不需要引入。
(3) 参看http://research.google.com/archive/mapreduce.html
(4) Python 2.7中,range()和map()返回的都是列表,所以是即时求值。










