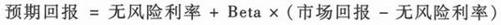预计阅读本页时间:-
第三节 投资风险的衡量
我们前面用百分数来表示的投资回报的标准差,是为了演示说明风险的相关概念。这些百分数并不是风险的直接衡量指标。为了计算资本成本,我们需要构建直接的风险衡量指标来具体化这个标准差的概念,并根据这个指标计算出资本成本的水平。
遗憾的是,风险看不到,摸不着。从理论上来讲很直观,现实衡量起来十分困难。直到20世纪50年代以后,通过Harry Markowitz和William F. Sharpe及其他金融学家的工作,我们才有一个衡量风险和计算资本成本的工具:资本资产定价模型(CAPM)。该模型可以写成以下的形式:
从这个模型中,我们看到决定资本成本(预期回报)的因素除了衡量风险水平的Beta以外,还有两个因素:无风险利率和(市场回报-无风险利率),我们称后者为风险溢价。
资本资产定价模型说明,资本成本由两个部分构成:一部分是无风险利率,用以补偿投资者资金的时间价值;另一部分是风险补偿,根据(不可分散)风险水平补偿投资者承担的投资风险。本小节讨论无风险利率和Beta,下一小节讨论风险溢价。
企业使用投资者资金首先要向投资者补偿资金的时间价值。资金的时间价值是指在完全无风险的情况下,投资者资金要求的投资回报。通俗地来理解,投资者的资金如果不用来投资,就会用来消费。只有消费才能给投资者带来效用。投资则推迟了投资者的消费。为了弥补投资者推迟消费而造成的效用损失,企业需要提供补偿。换句话说,一年以后的1元钱对投资者来说其效用要小于现在的1元钱,所以,如果要投资者现在放弃1元钱的消费,一年以后必须给他还回来多于1元的钱。差额就是时间价值。
衡量资金的时间价值的指标一般是无风险利率。我们通常用政府债券的利率作为无风险利率的代表[6],这是投资者在不承担任何风险的情况下投资可以带来的回报,企业首先必须补偿这部分投资者可以得到的回报,才能使投资者购买股票。
资本成本的第二部分是风险补偿,其由两个因素决定:第一是Beta,即不可分散风险水平;第二是风险溢价,即在无风险利率的基础上,每个单位的风险(Beta)需要补偿百分之几的预期回报。
William F. Sharpe的重要贡献之一是给出了Beta的衡量方法。[7]在资本资产定价模型的框架中,因为分散投资的作用,投资者只需要承担某只股票通过持有市场组合也分散不掉的系统风险,而股票的系统风险是由其回报与市场组合回报之间的相关性决定的。Beta衡量了这个相关性。
为了便于理解,我们先介绍对于一只股票来讲,Beta是怎样计算出来的。假如我们有股票A和市场指数(如标准普尔指数)过去60个月的月度回报,同时我们有这60个月中的无风险利率(5年期政府债券利率),这样,我们可以用这些历史数据作如下线性回归。
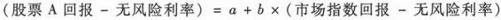
回归得到对a和b两个系数的估计值。b的估计值就是对Beta的计量,是股票A的不可分散风险水平,也就是说,是我们即使持有了市场组合也不能分散掉的股票A的风险。
为什么Beta是股票的不可分散风险(以后简称风险)的衡量呢?市场指数回报是市场组合的投资回报。我们前面介绍过,市场组合的风险是不能够被分散掉的风险(又叫系统风险),是投资者必须承担,而企业必须支付资本成本的风险。而一个股票的风险是指即使投资者通过持有市场组合也分散不掉的这只股票的风险。Beta衡量的就是这部分内容。例如,如果某只股票的Beta为1.5。这意味着如果市场指数上涨1%,股票上涨1.5%;如果市场下跌1%,股票下跌1.5%。所以,这只股票的系统风险是市场组合的1.5倍。显然,市场组合本身的Beta是1。Beta越大,股票的风险越高;Beta越小,股票的风险越低。[8]
下面我们从经济意义上来理解一下Beta作为风险衡量指标的含义。财富能够给人们提供效用,但是只有在消费财富的时候。例如,我们用财富去购买美味佳肴、华宅丽舍,去欣赏艺术品,去旅游,事实上,只有能够刺激我们物质感官的东西才给我们带来效用。我们称这种行为为消费(consumption)。对于绝大多数人来说,以纸币形式存在的财富并不直接带给我们效用。但是,消费的边际效用是递减的。随着对同一个目标的消费量的增加,每一个新增单位的消费带给我们的效用低于之前的一个单位的消费。例如,美味佳肴吃得过多不仅不会增加满足感,还会带来健康危害。这就是为什么人们有了钱不是马上全消费掉的原因之一。我们总希望每一个单位的财富都带来最大的效用。所以,我们放弃一部分现在消费,将这部分财富进行投资,以供未来消费使用。所以,在任何一个期间,我们可供用来消费的财富有两个来源:本期收入(工资、奖金等薪酬收入)和投资回报。
投资回报的高低取决于市场回报(对不可分散风险的补偿),而市场回报又取决于经济形势。一般来讲,薪酬收入和经济形势是正相关的,经济形势越好,人们收入越高;经济形势不好,人们收入降低,甚至被解雇。如果一只股票Beta很大,它的回报和市场回报及经济形势就具有很强的正相关关系。也就是说,这只股票在经济形势好的时候回报高,在经济形势差的时候回报低。而经济形势好的时候恰恰是投资者薪酬收入高、投资回报边际效用低的时候;经济形势差是投资者薪酬收入低、投资回报边际效用高的时候。所以,这样的股票“锦上添花、雪中不送炭”,因此风险大。相反,如果另一只股票的Beta很小,甚至是负的,其风险就小,因为它在经济形势好的时候回报低,但是在经济形势差的时候回报高。正好平滑了薪酬收入对消费的影响,增加了投资者的效用。
到这里,我们介绍了计算资本成本的资本资产定价模型,以及其中的无风险利率和风险水平Beta的计算方法。下一节我们介绍风险溢价,就可以完成资本成本的计算。
风险和资本成本看不见、摸不着,但是可以用资本资产定价模型(CAPM)衡量和计算出来。