预计阅读本页时间:-
计算几何经典问题
我们通过阐述一些经典问题来解释计算几何关注的领域。程序员要高效解决这些问题,首先必须理解一些在其他领域也非常有用的关键数据结构和算法技术。我们将会在阐述问题的过程中简单地描述和分析解决问题的原始算法,得知算法的期望运行时间。在本章剩余部分,我们将会提出一些更加优雅和高效的算法,这些算法也同样能够解决这些问题。我们再次重申,我们可以通过如下方法来改进算法:(a)利用问题的特殊信息。(b)在算法支持的范围内,寻找最合适的数据结构。
凸包
在二维平面上有一个点集P,凸包是能够包含P中所有点的最小凸多边形,在任意两点间画一条线段,凸包的边都属于这个线段集。有h个点的凸包是顺时针计算出来的,从L0到Lh-1,第一个点L0是P中最左边的点(虽然任意的点都可以作为起始点)[1]。顺着凸包上三个相邻的点Li,Li+1,Li+2,路线将会向右转,这种性质对于Lh-2,Lh-1,L0也成立。
广告:个人专属 VPN,独立 IP,无限流量,多机房切换,还可以屏蔽广告和恶意软件,每月最低仅 5 美元
给定n个点,存在C(n,3),或者:
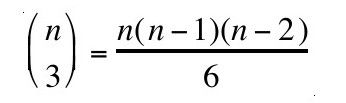
个不同的三角形。如果一个点pi∈P被P中其他三个点组成的三角形所包含,那么它不可能是凸包的一部分(例如,图9-4的点p6被包含在p4、p7和p8组成的三角形中)。一个穷举算法可以从这些三角形中一个一个地剔除点,然后得到凸包。一旦我们知道那些点可以组成凸包,那么接下来以最左边的点为起始点(p0)画一条线L0,然后将每个点pi和p0连成一条线Li,根据Li和L0的夹角从小到大进行排序,然后依次将这些点连起来即可。我们需要考虑到共线的情况。
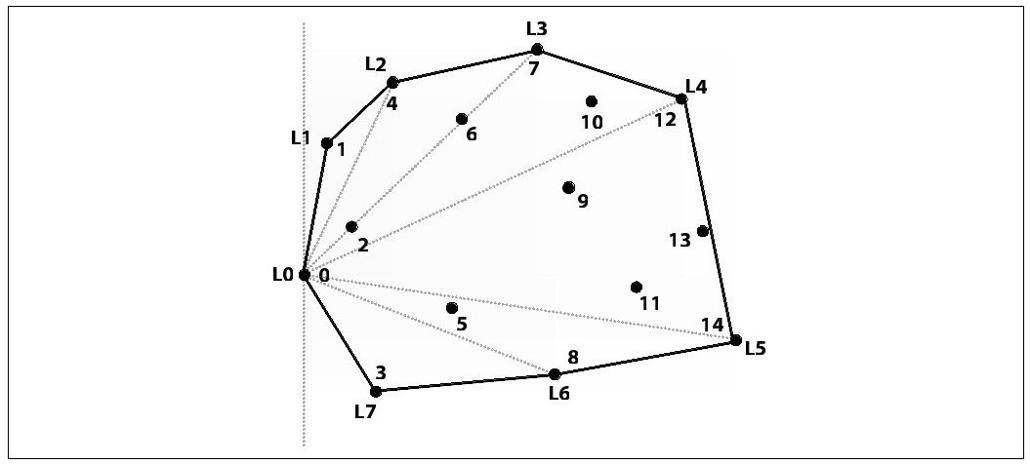
很明显这种方法非常低效,在三角形检测时就需要O(n4)的时间。接下来我们将会给出一个高效的凸包扫描算法,能够在O(n log n)的时间内计算出凸包。
计算线段集的相交
在一个二维平面上有一个线段集S,找出所有线段之间的交点。我们也许只想知道是否存在至少一个交点(可能会在找到第一个交点之后终止算法)。在图9-5的例子中,我们找到了两个交点。图9-6的穷举算法在O(n2)的时间内能够找到所有的交点。


例9-1是穷举探测的一个实现。有C(n,2)个线段对,或者:
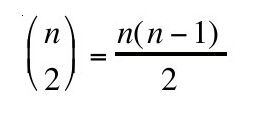
n个可能的线段对。对于每个线段对,下面的实现都会输出交点。
例9-1:穷举探测实现

其主要步骤需要O(n2)的时间。寻找两条线段的交点可能需要三角函数或者除法,这些都是开销非常大的操作,此外,如第3章所述,这些操作经常会引发一些舍入的错误。我们将会使用一种新的方法来检测交点,这种方法只使用加法、减法、乘法以及比较操作(Cormen等,2001)。
在之前我们不清楚是否可以通过一些改进得到优于O(n2)的性能,所以本章将会介绍一种创新型的线段扫描算法,其在平均情况下能够在O((n+k)log n)时间内得到结果(k是得到交点的个数)。
寻找最近邻点
我们可能要回答这类问题:“在二维平面上有一个点集P,以欧几里德距离为点之间的距离,P集合中离x最近的点是哪个?”当然x可能不在P中。
我们计算x和P中所有其他点的距离。这需要O(n)步。如第5章所述,二叉树能够帮助查找不去考虑那些不可能成为解的点。我们用树结构切分平面上的点,减少查找时间。查询所节省的时间能够补偿预处理的额外开销,我们能够在O(log n)的时间内得到结果。如果查询的次数比较少,那么O(n)的穷举方法可能更加好一些。
回答基于范围的查询
这种查询并不是在二维平面内寻找特定点,而是希望知道给定的矩形区域是否包含所有的点。最简单的实现需要花费O(n)的时间来得到解。
处理最邻接点的数据结构在这里也同样适用。我们如果希望能够在O(n)的性能上继续改进,必须做到(a)从候选点集中舍弃一部分。(b)候选点集需要包含结果可能有的点。我们在这里使用kd树这种数据结构,进行递归的遍历查询,这种实现的性能是:
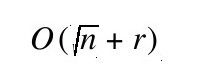
r是得到的点的数目。
总结
下述代码遵从表9-2的API定义。同时这个表也总结了本章描述的算法的性能。











