预计阅读本页时间:-
估算搜索树的大小
如果在同一个棋盘上的两个皇后在同一行、同一列或者同一对角线上,则它们可以互相攻击。接下来我们要将一个集合的皇后放置在棋盘上,并且让其中任意两个都不会互相攻击。很明显,我们不能把n+1个皇后放在n×n的棋盘上,因为两个皇后不能在同一行。我们总能放置n个不会互相攻击的皇后吗?这个问题就是有名的n皇后问题(n-Queens Problem)。我们来一般化这个问题,计算在一个n×n的棋盘上有多少种方式可以放置不会互相攻击的n个皇后。我们将要介绍的随机方法的应用不仅于此,除了我们这里谈到的游戏之外,还有很多应用,它能够用来估计搜索树的形状。
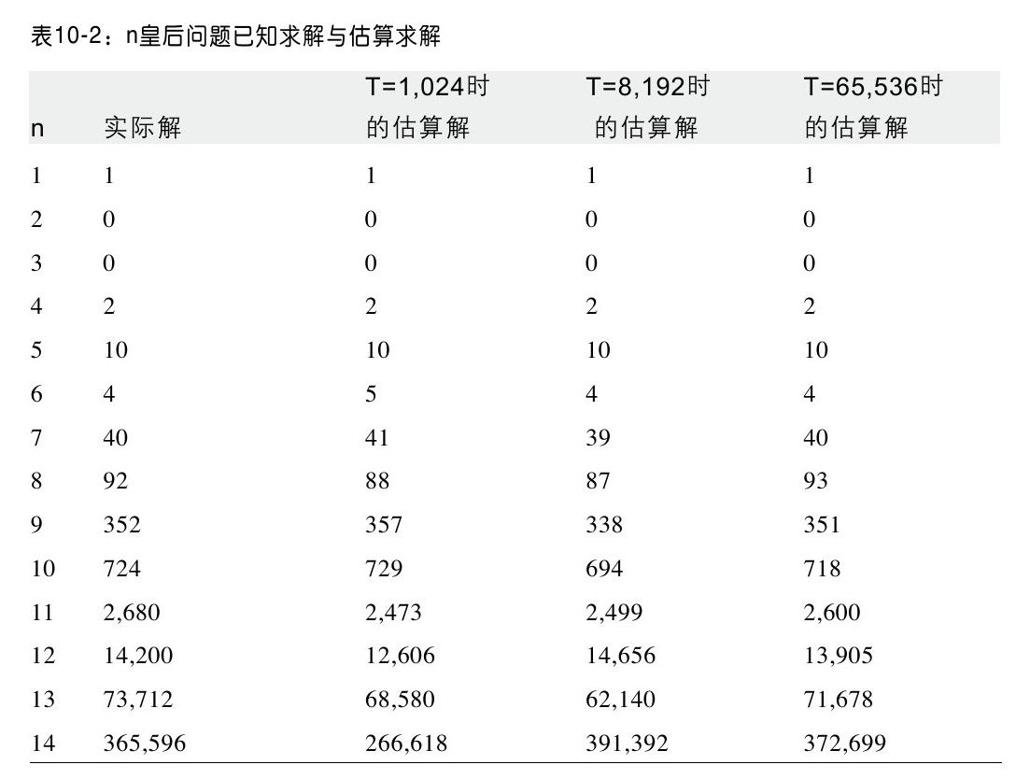
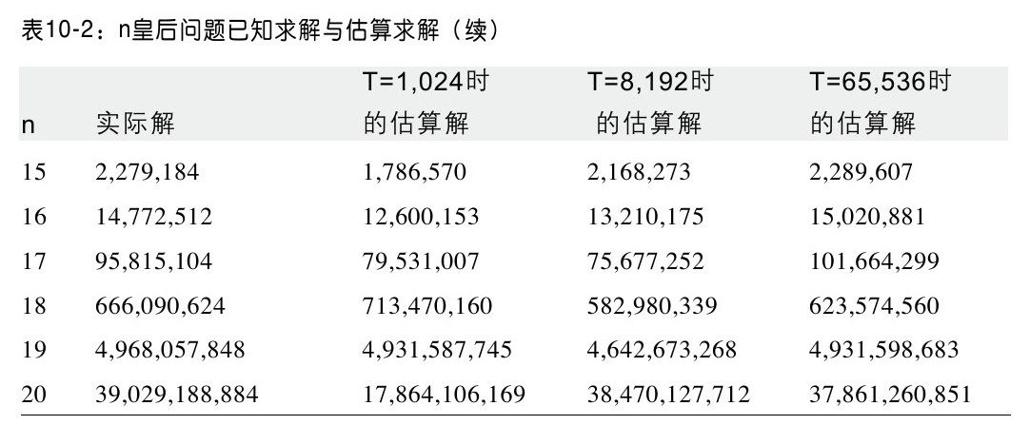
目前没有已知的技术可以高效地求解n皇后问题。表10-2所包含的数据是早些时候Sloane的整数序列在线百科全书所计算的[1]。
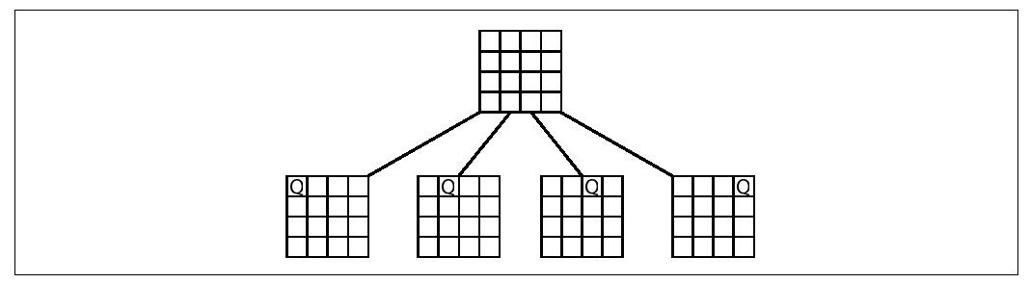
为了求出4皇后问题的精确解,我们基于每行只能有一个皇后的事实,生成了一棵搜索树。起始状态是没有放置任何皇后,图10-1展示了如何通过在第一行上依次摆下4个皇后来对搜索树进行直接扩展。
广告:个人专属 VPN,独立 IP,无限流量,多机房切换,还可以屏蔽广告和恶意软件,每月最低仅 5 美元
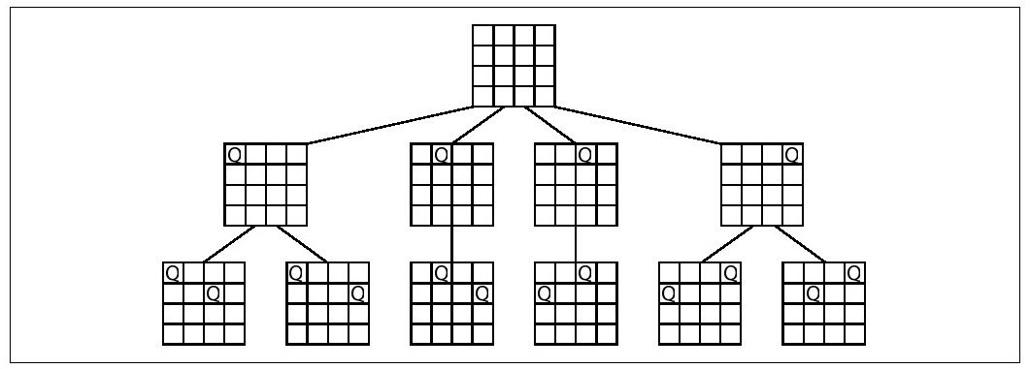
对每种情况再进行扩展,在第二行摆上不会互相攻击的另一个皇后,如图10-2所示。
第一个和最后一个中间解不能再放下第三个皇后了。中间的四个可以放置第三个,而最中间的两个则可以放置第四个皇后(如图10-3所示)。
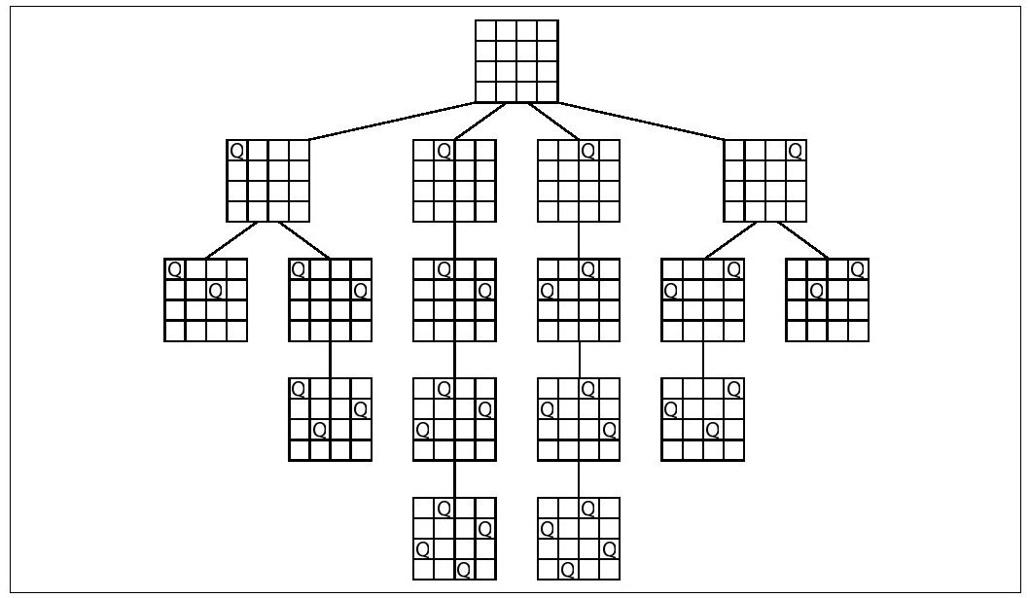
如此详尽地阐述搜索树让我们看到,4皇后有2个解。通过计算来解19皇后就难得多了。在第19层搜索树上,有4 968 057 848个节点,而整个树的节点更多,需要很长很长时间才能算出结果。
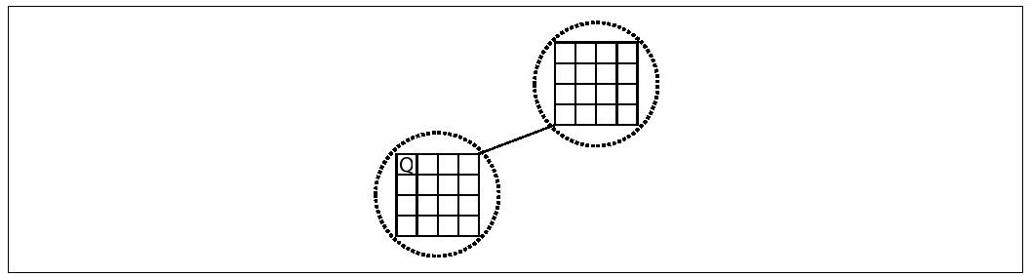
Donald Knuth(1975)提出了另一种全新的方法来估算搜索树的形状和大小。它的方法会随机地向下遍历搜索树。为了简洁起见,我们将会用4皇后来说明这个方法,明显地,它可以轻易地应用于估算19皇后问题的解的数量。从搜索树的根开始(没放置任何皇后),我们估计出在第0层有1个节点。接下来,我们会在所有节点上去确定其儿子节点的数量(由该节点所对应的中间解的直接扩展的数量),并且随机地选择它们。我们看到根节点有四个孩子,因此我们(正确地)估计在第1层有4个节点。接下来,我们随机地选择四个中的一个节点,比如说第一个,如图10-4所示。
对于当前随机路径的更低层节点,我们要查看它有多少个子节点(在第二行有多少种方式放置一个皇后),再随机选择其中一个。注意到它有两个孩子,我们估计在下一层的节点数是第1层节点数的两倍。也就是说,我们估计在第2层有8个节点,接下来我们在两个节点中随机选择其中一个,如图10-5所示。
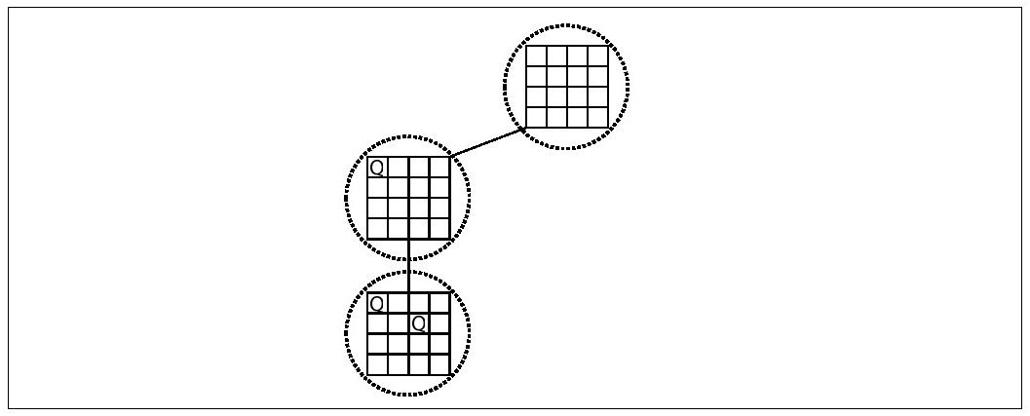
现在,当前随机路径的最低层节点,我们来确定其子节点的数量:能够有多少种方法放置第3个皇后?答案是0个,我们估计第3层节点的数量是第2层的0倍。也就是说,我们估计第3层有0*8个节点,那么在第4层就有0个节点。这说明我们估计出4皇后问题无解。事实上有些随机遍历并不准确,但是如果我们多次随机遍历,并取这些估计的平均,就会得到越来越接近真实值的结果。因为每一次估算是可以快速完成的,因此最终的(平均)估计值也可以快速求解的。每次估计的目标值都是正确结果,然而估计的平均值却可能随着增加尝试的次数更逼近正确答案。表10-2列出了我们所实现的算法的计算结果,分别为1024次、8192次和65 536次尝试。未包含时间信息,因为所有的结果都是一分钟内完成。19皇后问题T=65 536次尝试的最终估计值和真实结果相差3%。事实上,所有T=65 536的估计与真实值的差异都在5.8%以内。这个算法的特性就是,尝试的次数越多,最终计算的结果与真实值就越准确。例10-2展示了单次计算n皇后估计的Java实现。用于生成表10-2的完整代码存于代码库中。
例10-2:Knuth的随机估计n皇后算法的实现












